На досуге. К теории Риска. Финишировали!
Ох и утомился я тут, комментируя один пост...
Хочется написать и поговорить, о чем-нибудь любимом и приятном. Возможно, на досуге, между экспедициями в горы, мне, наконец, удастся продвинуть на этом сайте теорию о Риске. Иначе, какой же это Риск без теории Риска? :))
Недавно мой старший сын принес на обсуждение за чашечкой чая очередной тульский пряник и
задачку про двух заключенных.
Задача эта парадоксальная, особенно после того, как я поправил в ней некоторые цифры. И она интересна для опроса. Мало ли, как всё сложится...
Поэтому прошу максимально вдумчиво и ответственно проголосовать, прежде чем читать комментарии.
Как говорят, прочувствуйте ситуацию.
Итак, два заключенных сидят в СИЗО, общаться между собой они не могут. Каждый из них знает про такой расклад:
Если оба заключенных будут молчать - обоим сидеть по 1-му месяцу.
Если оба заключенных все расскажут - обоим сидеть по 6 месяцев.
Если один из заключенных будет молчать, а другой всё расскажет - то молчуну впаяют 8 месяцев, а рассказчика немедленно отпустят.
Вот как это выглядит на картинке:
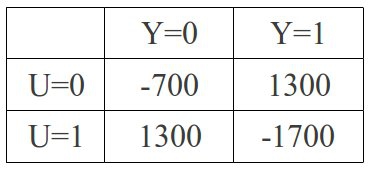
В табличках прописаны сроки лишения свободы для каждого из заключенных, при вот таких действиях:
U0 - заключенный U молчит,
U1 - заключенный U говорит,
V0 - заключенный V молчит,
V1 - заключенный V говорит.
Разобравшись в своих предпочтениях, я пригласил на следующий день Сашу на новую чашечку чая с брусничным вареньем и немедленно предложил сыграть.
О том, что из этого получилось, я расскажу позже.
Вот так мы провели первое и пока единственное испытание. А вот как поведет себя население в среднем? Вот, в чем вопрос...
Понятно, что это не простое население, это аудитория Риска, со всеми специфическими особенностями. :)
Итак, каждому в опросе предлагается представить, что он находится в КПЗ, и что в соседней камере сидит знакомый, которому угрожает та же участь, что и вам. Требуется выбрать одно из двух:
"Буду молчать" (U0)
"Всё расскажу" (U1).
Туристы в страшном ледопаде. Они мирно жуют курагу и просчитывают свои риски. Они не подозревают, что к ним уже подкрался неотвратимый ......
Ну что, проголосовали?
Тогда дальше...
В тот же день я раскопал парадокс о двух конвертах, который поверг меня в замешательство и надолго выключил из растительной жизни. Отправляясь на работу, Саша поцеловал меня и сказал: "Спасибо, папок, давненько в жизни не было ничего интересного, пойду поразмышляю о двух конвертах".
Парадокс о двух конвертах.
Коля положил в два одинаковых почтовых конверта некоторую сумму денег, причем в один из них ровно в два раза больше, чем в другой. Потом он подбросил монетку и, повинуясь случаю, один из конвертов вручил Васе, а другой Пете.
Вася открыл конверт, пересчитал деньги и подумал так: "У меня в конверте сумма X. Значит, с вероятностью 0.5 в конверте у Пети лежит сумма X/2 и с вероятностью 0.5 он обладает суммой 2X. Выгодно ли мне меняться? Ожидаемый выигрыш от обмена конвертами равен: 0.5 * (X/2 - X) + 0.5 * (2X - X) = 0.25 * X > 0. Значит, меняться выгодно!"
Аналогично может рассуждать и Петя. Получается, что меняться выгодно обоим. Но ведь, это же лажа!
О проведенном мною исследовании этого парадокса я расскажу позже, к его правильному восприятию необходима предварительная подготовка.
А ночью мне приснился странный пример, когда одна случайная величина содержит информацию о другой, а та другая не содержит информации о первой. Я сейчас объясню, почему это странно.
Дело в том, что в обычной теории вероятностей отсутствие информации эквивалентно взаимной независимости случайных величин, а значит, ситуация с отсутствием информации симметрична. Действительно, случайная величина X не содержит информации относительно случайной величины Y, если и только если, X и Y независимы, а это, в свою очередь, необходимо и достаточно для того, чтобы случайная величина Y не содержала информации о случайной величине X.
Однако в теории вероятностей взаимное распределение случайных величин X и Y считается известным. Совсем иначе, если мы имеем дело со статистически неопределенной ситуацией.
Вот, какой пример мне приснился:
Две бинарные (т.е. принимающие два значения 0 и 1) случайные величины X и Y имеют совместные распределения, которые отражены табличками. Распределений два. Случайная величина X принимает значение 0 с вероятностью 2/3 и значение 1 с вероятностью 1/3 независимо от распределения. А вот случайная величина Y принимает свои значения с вероятностями 2/3 и 1/3 уже в зависимости от распределения. При первом распределении (V=0) более вероятно значение Y=0, а при втором распределении (V=1) более вероятно значение Y=1. Какое из распределений истинно - не известно.
В этом примере случайная величина X содержит информацию о случайной величине Y, но не наоборот, случайная величина Y информации об X не содержит.
"Мама, а розочка бывает больше самолёта?" "Что ты, Вовочка, розы намного меньше самолёта". "Даже если один шанс на миллион?" "Розы всегда меньше самолёта". "А почему папа сказал, что шанс один на миллион, а самолёт опять розочкой накрылся?"
Попробую объяснить этот пример.
Но для этого сначала расскажу о рандомизированных стратегиях.
Однажды участник нашего памирского похода меня спросил: "А почему ты в одинаковых ситуациях принимаешь разные решения, то так, то эдак?" В ответ я отшутился: "Это потому, что я использую рандомизированные стратегии". Тогда я осознал, что о рандомизированных стратегиях, увы - мало кто знает...
Рандомизированная стратегия, это когда вы кидаете монетку, чтобы принять решение. Во многих задачах она позволяет получить оптимальный гарантированный результат и подсказывает самый рациональный способ поведения. Когда, еще будучи студентом, я впервые узнал об этом, то это стало революцией в моей голове! Представить, что оптимальное поведение требует инструмента в виде мешочка с костями...
Представить такого я не мог.
Рассмотрим такую задачку:
U=0 или U=1 - это два варианта вашего решения. Y=0 или Y=1 - это два возможных значения неизвестной вам величины. Это могут быть непредсказуемые действия другого человека или какой либо иной параметр, который, если и можно считать случайным, то о его распределении, всё равно, ничего не известно. А в табличке проставлены суммы денег, которые вы можете выиграть или проиграть.
Как бы вы себя не вели, от проигрыша, всё равно, не застрахованы. Если выберете U=0, то можете проиграть 700 рублей. А если выберете U=1, то можете проиграть 1700. При равных выигрышах решение U=0 безобиднее, поэтому и выглядит предпочтительнее.
Однако существует способ извлечь из этой ситуации положительный в среднем выигрыш! Иначе говоря, при многочисленных повторениях этой игры вы начнете обогощаться, как бы не вела себя величина Y. Единственно, что не разрешается в этой задачке, чтобы Y "подсматривала ваши решения" и уже после каждого вашего выбора нагло подсовывала вам проигрыш. :)
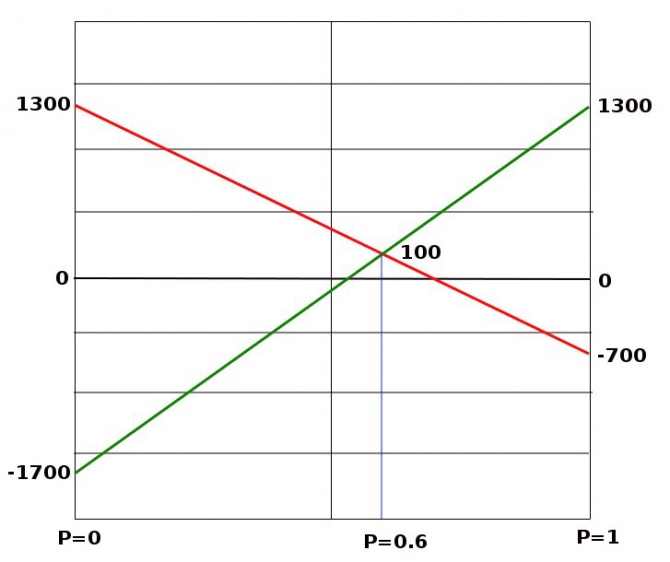
Давайте принимать решение U=0 с вероятностью P и решение U=1 с вероятностью 1 - P. Тогда при Y=0 ваш ожидаемый выигрыш равен:
Q = -700 * P + 1300 * (1-P) = 1300 - 2000 * P.
А при Y=1 ожидаемый выигрыш равен:
Q = 1300 * P - 1700 * (1-P) = 3000 * P - 1700.
Первый выигрыш падает с ростом P, а второй растет.
Вычислим P, при котором эти выигрыши уравниваются. Легко убедиться, что равенству соответствует P = 3/5 = 0.6 . При такой вероятности, в обоих случаях, независимо от значения Y, ожидаемые выигрыши равны 100 руб. > 0. Стоит, хоть немного отклониться от этой вероятности, как вы рискуете получить ожидаемый выигрыш меньше 100 рублей или даже реально проиграть.
Вот так.
Кидайте монетку, господа!
Это и есть рандомизированная стратегия.
Вы можете себе представить, что наилучший ледоруб состоит из двух ледорубов? Наклейка одна: BD-22, а ледорубов два, и разной конструкции. Один вам приносят со склада с вероятностью 0.6, а другой с вероятностью 0.4 :))))
Продолжение следует...
Обсуждение парадоксов, расчеты и результаты голосования оформлены в отдельной статье на моей личной ленте вот ЗДЕСЬ:
1. А. Лебедев. Анализы парадокса о двух конвертах и задачи о двух заключенных.
188
Комментарии:
Войдите на сайт или зарегистрируйтесь, чтобы оставить комментарий





Вот опилки в голове чуть подсохнут ---постараюсь вникнуть :--)))
Что за единица измерения такая: вероятность умноженная на рубль – математическая или физическая? :)
Парадокс конвертов раскрыт. Он обусловлен стиранием границ между виртуальностью и реальностью :)
Пусть у вас есть лотерейный билет, который обеспечивает вам 100 рублей с вероятностью 0.5 и 0 рублей с вероятностью 0.5
Ожидаемый выигрыш равен 50-ти рублям.
Не сомневаюсь, что большинство людей предпочтут реальных 50 рублей такому билету. Но за сорок рублей его купят многие. А 100 таких билетов по цене в 40 рублей только дурак не купит.
С ростом числа испытаний N разница между реальными и, как вы говорите, виртуальными деньгами исчезает. Виртуальная сумма миллиона таких билетов отличается от реальной суммы в 50 миллионов рублей не более чем на 0.3 процента (т.е. 0.003) с вероятностью 0.997 (посчитал устно, но, вроде, не ошибся).
В голосовалке не принимал участие, т.к. не хватает исходных данных. Если заключенный №1 чувствует симпатию, сострадание, испытывает уверенность в заключенном №2, то он, скорее всего, промолчит. А если испытывает недоверие, то заложит.
Выйграть можно только изначально обладая меньшей суммой чем у товарища (т.е. 1/2Х), следовательно вместо 0.5 * (X/2 - X) + 0.5 * (2X - X) = 0.25 * X, надо писать 0.5 * (X/2 - X) + 0.5 * (X - Х/2) = 0 * X, и иллюзия исчезает..
А задача такая интересная получилась:)
Если бы выигрыш/проигрыш был бы не во сколько-то раз, а на сколько-то рублей, оптимальным решением было бы не меняться, но, когда в два раза - появляется смысл.
Рассмотрим такой пример: в конверте у меня 10 рублей, а у Васи может быть в 1000 раз больше. Если мне повезет, то я получу каккие-то деньги, а если нет - бог с ними с 10 рублями.
Правда, в этом случае, Вася должен тоже абстрагироваться от уровня своих доходов и доходов подарившего конверт, иначе он быстро придет к выводу, что меняться не стоит.
Этот парадокс имеет место быть только в том случае, когда речь идет о суммах не значительных для играющих, когда же речь пойдет о больших суммах (дарящий - миллионер), и Вася и Петя будут бояться проиграть больше, чем выиграть, а ваша формула этого не учитывает, она чисто математическая. :)
Если мне повезет, то я получу какие-то деньги, а если нет - бог с ними с 10 рублями.
Это о полезности каких то значимых денег и бесполезности десятки.
Давайте не будем припутывать к парадоксу понятие полезности, ведь можно считать, что в конвертах с самого начала заложены не деньги, а полезность (полезность - известное понятие в исследовании операций, применительно к деньгам - это нелинейная функция денег, осреднение которой по вероятности считается осмысленным).
Все работает: и Вася и Петя в, любом случае, выигрывают в 2 раза больше, чем проигрывают.
И чего они там навыигрывают, когда начнут меняться при полностью симметричной ситуации?
Однако вы очень близки..
Интуиция славная.
Когда увидите решение - порадуетесь! :)
"Полезность" надо либо включить в формулу, что очень непросто, либо исключить вовсе, тогда надо оговорить условия среды в которой имеем парадокс (перед вами живые люди, а не математики, они по себе меряют.)
Если мы говорим об оптимальных решениях, оптимальные решения бывают только для каких-то текущих условий и эти условия необходимо оговаривать отдельно, тогда "полезность" стоит учесть.
А ведь поначалу мозг сводит. :))
Вот к чему приводит не знание бухгалтерии и не корректная постановка задачи. Доходы и расходы можно складывать только по-отдельности. Доход - 100 р. у друга + 50 р. у подруги = 150 р. Расход - 100 р. пропил(ладно, потерял) + 30 р. отдал другу + 20 р. шоколадки = 150 р.
Сальдо: 0.00 р.:-)
(Это в струю замечания №2 в моем посте ниже, которое является общим.)
Игрушечная машинка с заводным ключиком массой m=2 кг развивает скорость V=1 м/c. Большая машинка? Ну да ладно, так легче считать.
Её кинетическая энергия равна m*V*V/2 = 1 джоуль. Ясно, что эта энергия запасается в пружине, а потом переходит в кинетическую энергию машинки.
Мальчик запустил машинку в поезде, который движется со скоростью 10 м/c.
Относительно земли машинка имела до старта скорость 10 м/c, а после своего жужжащего разгона - скорость 11 м/c.
Её кинетическая энергия возросла от 100 джоулей до 121 джоуля.
Откуда взялись лишние 20 джоулей? :))
1. Из поезда.
2. Если взятая модель противоречит реальной действительности, значит она выбрана неправильно и необходимо искать другую модель.
3. А "поначалу" (в заметке выше) пишется слитно.
2). Принцип относительности в механике утверждает, что все механические процессы протекают одинаково в любой инерциальной системе отсчета. Поэтому школьник должен уметь работать в любой системе координат.
3). Спасибо, исправил :)
покончим со школьным парадоксом о кинетической энергии.
Представим, что поезд движется с выключенным двигателем, по инерции. Взаимодействуя с поездом, машинка сообщает ему микроскопический импульс и чуточку тормозит его. В результате кинетическая энергия поезда убывает на 20 джоулей. Закон сохранения энергии выполняется.
Проверим это. Запишем закон сохранения импульса:
(m+M)W = M(W-d) + m(W-d+V),
где m = 2 кг - масса машинки
M - масса поезда
W = 10 м/с - скорость поезда до запуска машинки
d - изменение скорости поезда
V = 1 м/c - скорость машинки относительно поезда.
Из этого уравнения следует, что
d = mV/(m+M) - ничтожная величина.
Однако разность кинетических энергий поезда до запуска машинки и после её разгона равна:
MW*W/2 - M(W-d)(W-d)/2 = MWd - Md*d/2 ~ MWd = MWmV/(m+M) ~ WmV = 10 * 2 *1 = 20 дж.
Если скорость поезда после разгона машинки не изменилась, значит двигатель разогнал поезд с W-d до W и совершил работу в 20 джоулей.
И закон вообще-то нельзя записывать для состояний "до" и "после" внешнего воздействия ( в данном случае, толчка машинки).
Товарищ, не вешайте лапшу на уши. В реальной жизни вы ничего и никогда не посчитаете, если будете сравнивать поезда и заводные машинки. Расчётная модель у вас будет перегружена.
Я прошу на меня не накладывать штампы, что я должен знать а что нет.
Впрочем, ладно, можете накладывать. Но потом не обижайтесь, что сами станете штампом.
А вот формулировка еще круче. Нет никакого поезда. Есть инерциальная система отсчета, которая движется навстречу игрушке со скоростью 10 м/c.
До запуска, скорость игрушки в этой системе отсчета равна 10 м/c
После отработки пружины (а машинка просто проехалась по асфальту) скорость машинки в этой системе отсчета 11 м/c
Разность кинетических энергий 121 - 100 = 21 джоуль.
Откуда взялись лишних 20 джоулей?
Земля вместо поезда, только и всего :)
****
В детстве мне нравилась идея остановить вращение земли.
для этого предполагалось людям всем разом пойти на восток, заодно в ту же сторону поехать автомобилям и паровозам:)
До воплощения идеи дело не дошло,
и хорошо,
а то вдруг бы получилось... жили бы сейчас на планете где с одной стороны горячая сковородка, с другой- морозильник.:))
Земляне , забыв склоку капитализма и коммунизма,разделились бы на два племени,
У одних в крови тек бы жидкий азот, у других плазма:))
Был маленький "Доктор Зло"?:-)))
Мальчик, заводящий пружинку, тоже в поезде сидит, и его импульс входит у Андрея в уравнение (как составная часть MW), поэтому он никакая не внешняя сила, а внутренняя.
*****
считать надо вместе, машинку и поезд.
Общая энергия системы не изменилась
Разгоняясь, отталкиваясь от поезда машинка притормозила поезд и его энергия уменьшилась на эти 20 джоулей.
Тогда я задал ему аналогичную задачку уже без поезда.
Чтобы уж совсем... :)))
Вот про поезд еще. Если машинка разгоняется до 1 м/с за 2 секунды, то она воздействует на поверхность с силой 1 ньютон (2 кг * 0.5 м/c*c = 1 н). За 2 секунды поезд проезжает 20 метров. Работа машинки по торможению поезда равна F * S = 1 н * 20 м = 20 джоулей.
Опять все те же 20 джоулей!
А мощность 10 ватт !!! Ха-ха-ха!
Ну а если в постановке без поезда. Нет никакого поезда. Есть инерциальная система отсчета, которая движется навстречу игрушке со скоростью 10 м/c.
До запуска, скорость игрушки в этой системе отсчета равна 10 м/c
После отработки пружины (а машинка просто проехалась по асфальту) скорость машинки в этой системе отсчета 11 м/c
Разность кинетических энергий 121 - 100 = 21 джоуль.
Откуда взялись лишних 20 джоулей?
Вон выше расчет этой силы и работы поезда. Как раз 20 джоулей.
А расчет выше - совершенно правильный.
Всё, не буду больше занудствовать :-)))
****
Зачем при равномерном движении работа двигателя?
Вы ж не собираетесь учитывать трение, задача ведь не о том
Давай не будет поезда. Машинка запускается по асфальту. Процесс рассмотрим в системе координат, которая движется навстречу машинке со скоростью 10 м/с.
В этой системе координат сила трения от колес машинки совершает над Земным Шаром работу в 20 джоулей.
А если система координат будут двигаться со скоростью 20 м/c, то та же самая сила произведет над Земным Шаром работу в 40 джоулей.
Я подозреваю, что многие не верят в воздействие машинки на Земной Шар и думают, что я гоню пургу. На самом деле это всё очень серьёзно. :)))
Е.И. Бутиков, А.А.Быков, А.С.Кондратьев. Физика в примерах и задачах. Санкт-Петербург, "Лань", 1999.
******
машинка толкает землю.
Как Бог свят.
И мы толкаем.
Хорошо, что в разные стороны - а то- бяда:)
*****
Есть другой вариант- не знаешь, что делать- действуй по плану
"После просмотрa пaртиотического фильмa учитель спрaшивaет у детей, кому кто понрaвился. Одному подвиг солдaтa, другому - кaк сaнитaркa рaненого спaслa. А Вовочкa говорит:
- А мне больше всего понрaвился нaркомaн.
- Кaкой тaкой нaркомaн. Тaм не было нaркомaнов.
- Был, он все время зaтягивaлся и говорил: "Хороший у вaс плaн, товaрищ Жуков!"
Мужчины бросились в вычисления- один щанс на миллиард или триллион...
Женщины сказали "50%- либо встречу, либо нет" :) (старый бородатый анекдот.)
" Мужик с убитым видом пришел в мaгaзин. Спрaшивaет (грустно):
- Дaйте мне мыло и веревку...
Продaвщицa:
- Вешaтся, что-ли собрaлся?
Он (язвительно):
- Нет, б_я, счaс помоюсь вот - и в горы..."
"Два альпиниста наконец-то вылезли на вершину Эвереста. И один, вытирая пот с лица, спрашивает другого:
– Ну как, у тебя получилось с тем обменом квартиры?
– Да я чё псих — пятый этаж без лифта?!"
совместные потери: молчать - 2; 8, говорить - 8; 12, то есть выгоднее молчать.
Надо напарнику перед восхождением давать такие задачи :)
****
Я бы пошел только с таким, который даст определенный ответ.
Других- нах :)
*****
Я не слышал.Интересно, где?
Зато недавно впервые услышал про откат в 100% от стоимости работ, по конкретному объекту.
Растем понемногу :)
Это на риске звучит как "останетесь вы членом команды, или поступите, как сейчас модно" (модно, например, на зимне-весенних коммерческих и прочих интернетно-случайных восхождениях на Эль).
Тенденция настораживает. Среди посетителей риска целая толпа "вот этих вот": U1 (всё расскажу) 16.28% (14)
Как рассуждает Вася?
Он рассчитывает ожидаемый выигрыш от обмена конвертами. Такое среднее в теории вероятностей называется математическим ожиданием выигрыша.
Какая интерпретация полученной величины?
Интерпретация достигается мысленным погружением в гипотетический ансамбль повторяющихся ситуаций.
Например, если вы обладаете лотерейным билетом, который выигрывает 100 рублей с вероятностью 0.5, математическое ожидание выигрыша равно 0 руб. * 0.5 + 100 руб. * 0.5 = 50 руб. При многочисленных играх с билетом такого номинала вы получите примерно N* 50 руб., где N - число игр, причем, чем больше игр, тем меньше относительная ошибка в прогнозе дохода. Если N - миллион, то ваш доход будет отличаться от 50-ти миллионов рублей менее, чем на 0.3 процента (0.003) с вероятностью 0.997.
Вот и Вася мысленно погружается в гипотетический ансамбль повторяющихся ситуаций с обменом конвертами.
Но каков источник случайности в этих будущих его играх? Судя по тому, как он ведет расчет, единственным источником случайности он считает монетку, которую подбрасывает Коля. А количество денег в конверте X, он не усредняет по какому-либо распределению вероятностей и считает его, как бы, фиксированным.
Однако величина X Васе заранее неизвестна, как и все её будущие значения. Такое частичное осреднение, которое произвел Вася, при фиксированном X, в теории вероятностей называется условным математическим ожиданием, "математическое ожидание при условии, что величина X принимает наблюдаемое значение".
Является ли условный ожидаемый доход критерием рационального выбора?
Да, если мы имеем дело со статистически определенной ситуацией, т.е., когда вероятности всех фигурирующих в модели событий заранее известны.
В этом случае безусловное математическое ожидание выигрыша равно условному ожиданию, усредненному по распределению случайной величины X. Поэтому, если условное ожидание выигрыша при каждом фиксированном X максимально, то максимальным будет и безусловное ожидаемое значение выигрыша.
Может быть на это рассчитывал Вася?
Но тогда он неправильно посчитал свой выигрыш. Он не учел распределения величины X.
А без этого нельзя. Предположим, что используемый Колей капитал не превосходит 300 рублей. К примеру, пусть сумма денег в обоих конвертах Z распределена равномерно от 0 до 300 рублей. Тогда, если Вася увидел в своём конверте 110 рублей, он уже не должен меняться. Ведь у Пети может быть только 55, но никак не 220 рублей (110 + 220 > 300).
А между тем Васин расчет показывает положительный условный выигрыш при любом значении X, и при любом распределении этой случайной величины.
Чему же соответствует Васин расчет? Какому гипотетическому ансамблю?
А вот какому. Васе постоянно кладут в конверт 100 рублей, а Коля с вероятностью 0.5 кладет в конверт Пети то 50, то 200 рублей. Но это несимметричная ситуация, и никакого парадокса нет. Васе каждый раз выгодно меняться, а Пете нет.
100 рублей - это к примеру. Речь может идти о 200 рублей или иной сумме, но, главное, что эта сумма в гипотетическом ансамбле повторяющихся ситуаций остаётся фиксированной.
Однако это не интересный случай.
Исследуем задачу при некоторых стандартных распределениях суммы денег Z в двух конвертах.
Оказывается, что парадокс в некотором смысле сохраняется, и обоим игрокам при определенных ограничениях выгодно меняться. В Википедии ничего не говорится о возможности такой ситуации.
Итак, пусть сумма денег Z, которую Коля тратит на эксперимент, случайна и имеет функцию распределения F(z). Пусть независимая от Z бинарная случайная величина T принимает значения 0 или 1 с вероятностями 0.5 и отражает, кому досталась меньшая часть денег, т.е. Z/3: если Васе, то T = 0, если Пете, то T=1.
Пусть X - сумма в конверте Васи. Найдем функцию G(x) распределения случайной величины X.
G(x) = P{ X < x } = P{ X < x, T = 0} + P{ X < x, T = 1} = P{ Z/3 < x, T = 0} + P{ 2Z/3 < x, T = 1} = P{ Z < 3x, T = 0} + P{ Z < 3x/2, T = 1} = 0.5 * F(3x) + 0.5 * F(3x/2).
Дифференциируя функцию распределения, найдем плотность распределения случайной величины X.
g(x) = 1.5 * f(3x) + 0.75 * f(3x/2),
где f(z) - плотность распределения случайной величины Z.
По формуле Байеса найдем условные вероятность (при условии X), что к Васе пришла меньшая сумма денег Z/3 или большая сумма денег 2Z/3.
P{ T = 0 | X } = f(3X) / [ f(3X) + 0.5*f(3X/2) ]
P{ T = 1 | X } = 0.5* f(3X/2) / [ f(3X) + 0.5*f(3X/2) ]
Как видно, эти вероятности вовсе не равны 0.5.
Условное математическое ожидание выигрыша Васи при обмене равно
Q(X) = X * P{ T = 0 | X } - 0.5 * X * P{ T = 1 | X } = X * [ f(3X) - 0.25*f(3X/2) ] / [ f(3X) + 0.5*f(3X/2) ].
Условный ожидаемый выигрыш положительный, если и только если 4 * f(3X) > f(3X/2).
Оптимальная стратегия Васи:
!!!!! Меняться, если 4 * f(3Х) > f(3X/2),
!!!!! Не меняться, если 4 * f(3Х) = H/3 = 100 руб.
Ожидаемый выигрыш при этом равен H/16 = 18.75 руб.
2) Пусть Z - распределена экспоненциально с математическим ожиданием S = 150 руб.
И для этого распределения нетрудно посчитать, что
оптимальная стратегия Васи:
!!!!! Меняться, если X < 2S * ln(4) / 3 = 138.6 руб.,
!!!!! Не меняться, если X >= 2S * ln(4) / 3 = 138.6 руб.
Ожидаемый выигрыш при этом равен S(1 + 2ln(4) / 3) / 32 = 9.02 руб.
Но ведь и у Пети тоже самое! Парадокс сохранился?
Вовсе нет. :)
Оптимальная стратегия Васи действительно оптимальна, если Петя ему не противодействует и соглашается на все обмены, которые ему предлагает Вася.
При такой пассивной со стороны Пети игре Вася действительно выигрывает с каждым обменом в среднем по 18.75 руб. при равномерном распределении и по 9.02 руб. при экспоненциальном.
И эти числа подтвердились на компьютере методом Монте-Карло!
И Петя посчитает для себя такой же положительный ожидаемый выигрыш. И этот расчет тоже будет справедлив только при пассивной игре Васи.
А что же получится при активной игре обоих игроков?
Часть выгодных для Васи обменов забракует Петя, потому что по его оптимальному критерию некоторые предложенные Васей обмены будут невыгодными. С другой стороны, часть выгодных для Пети обменов забракует Вася. В итоге, выигрыш каждого будет равен нулю. И это тоже подтверждено на компьютере методом Монте Карло.
Вот такое получилось интересное исследование.
Там обнаружилась еще одна интересная игровая деталь.
Но об этом, если и расскажу, то в другой раз.
После вручения конвертов вероятность обладания большей суммой денег для Пети и Васи равна по 0,5. Это статус кво возвращается после каждого обмена конвертами. Потому что на двух людей есть два конверта.
Это совершенно реальная вещь - влияние информации.
И совершенно реально у меня на компьютере Вася обыгрывает Петю, если Петя не сопротивляется.
Я же не формулы на компьютере считаю, я моделирую случайные числа, рассовываю из по конвертам, потом их вскрываю, Вася и Петя принимают решения и т.п. Это моделирование методом статистических испытаний или методом Монте Карло.
И все формулы таким способом проверяются.
Всё работает.
Рисковский редактор начинает глючить после символа "больше или равно" и выбросил часть текста из анализа парадокса. Пришлось изменить нестрогие неравенства на строгие. Исправить коммент уже невозможно. Поэтому для полноты картины вношу исправления здесь:
////////////////////////////////////
Условный ожидаемый выигрыш положительный, если и только если 4 * f(3X) > f(3X/2).
Оптимальная стратегия Васи:
!!!! Меняться, если 4 * f(3Х) > f(3X/2),
!!!! Не меняться, если 4 * f(3Х) < f(3X/2).
Рассмотрим два примера:
1) Пусть Z - равномерно распределена в интервале от 0 до H = 300 руб.
Для такого распределения нетрудно посчитать, что
оптимальная стратегия Васи:
!!!! Меняться, если X < H/3 = 100 руб.,
!!!! Не меняться, если X > H/3 = 100 руб.
Ожидаемый выигрыш при этом равен H/16 = 18.75 руб.
2) Пусть Z - распределена экспоненциально с математическим ожиданием S = 150 руб.
И для этого распределения нетрудно посчитать, что
оптимальная стратегия Васи:
!!!! Меняться, если X < 2S * ln(4) / 3 = 138.6 руб.,
!!!! Не меняться, если X > 2S * ln(4) / 3 = 138.6 руб.
Ожидаемый выигрыш при этом равен S(1 + 2ln(4) / 3) / 32 = 9.02 руб.
Но ведь и у Пети тоже самое! Парадокс сохранился?
////////////////////////////////////////////////
Вот этот кусок должен стоять вместо аналогичного, но ущербного (с потерей нескольких строк) куска в тексте анализа.
Проще всё, мне кажется.
Есть такая теорема:
Теорема о сложении вероятностей 1. Вероятность появления одного из двух несовместных событий равна сумме
вероятностей этих событий.
(A+B)= P(A)+P(B) , в нашем случае 0.5 * (X/2 - X) + 0.5 * (2X - X) = 0.5X-0.25X=0.25X Ты подсчитал по этой формуле,
а есть вот такая теорема:
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
P(A+B)= P(A)+P(B)-P(AB) и в нашем случае получается 0.5 * (X/2 - X) + 0.5 * (2X - X)= 0.5X-0.25X-Х=-0.75X
Вот это похоже на правду.
Несовместными называются события, которые не могут произойти одновременно. Классический пример - орёл или решка. одновременно выпасть они не могут.
Непонятно как по такому определению классифицировать совместные эти события или нет, но результат второй формулы ближе к природе это точно.
Хочется сказать что события эти совместны и значит пользуйся второй теоремой, и всё будет хорошо.
вот например априори, выгоду получит Вася, и получит Петя, совершенно независимо, но одновременно. С точки зрения стороннего наблюдателя события как бы совместны, могут перемножаться и пользуемся второй формулой.
Или если Коля шутник, и положил сумму Х=0 в конверт, значит вероятность получения выгоды от обмена независимо от первоначального расклада на самом деле ноль 0.5*0=0 и опять хочется перейти к тому что значит события эти совместны...
С другой стороны, казалось бы, независимые события это наш случай, ибо выгоду от Васи и выгоду от Пети вообще невозможно получить одновременно одному из них, без бандитизма если :)
Я, тем не менее, буду молчать, и меняться буду :)
Ты только к формулам не придирайся. :)
Так как анализировался парадокс, то я особо тщательно проверял все выкладки и даже не умом, а методом Монте-Карло. Вот все эти доходы в рублях, что я понаписал - всё это реализуется с точностью до 3-го знака (включительно) после 100 миллионов обменов. Вон в третьей строчке q0 - средний доход от одного обмена для Васи. По теории должен быть 18.75
Это было для равномерного распределения Z.
А вот для экспоненциального:
Теоретический доход Васи - см. в первой строчке Q.
Реализованный средний доход от одного обмена после 100 миллионов испытаний - см. в третьей строчке q0.
Или еще статистику пособираем?
заключенный доложен кинуть монетку
1) сколько "рассказчиков" на Риске завалило друг друга на 6 месяцев.
2) сколько "рассказчиков" на Риске завалило "молчунов" на 8 месяцев и, тем самым, выкрутились.
3) сколько "молчунов" на Риске отделались одним месяцем.
:))
Q1 = P (если V - молчит)
Q2 = 2*P+6 (если V - говорит)
Эти линии не пересекаются и оптимальной стратегии тут нет.
Наиболее близкой к оптимальной будет стратегия "все рассказать".
Я без всяких расчетов знаю- все зависит от личностей.
Склонный к риску и азартным играм поменяется, несклонный- ни за что, будет рад тому, что есть.
Аналоговое мышление эффективней:)
Эта задача классифицируется, как игра с непротивоположными интересами. К сожалению, я не много смогу о ней рассказать. В эту область науки я не углублялся.
Литература:
1. Ю.Б. Гермейер. Игры с непротивоположными интересами. Москва, Наука, 1976.
2. Игры с непротивоположными интересами: учеб. пособие. Сост. Р.Ф. Хабибуллин – Казань: Казан. гос. ун-т, 2009.
Первая книжка - серьезная монография.
Вторая - простенькое пособие для студентов с обзором основных постановок.
Ну что я могу сказать? Дурная задача, и в этих книжках ничего толком о ней не сказано.
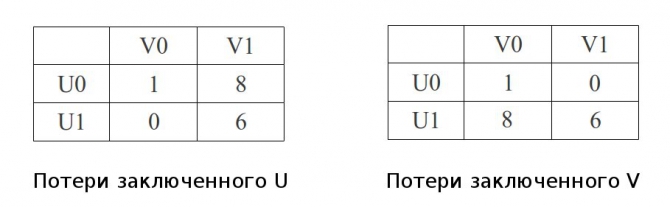
1) Обращаю внимание на то, что стратегия U1 ("рассказать") доминирует стратегию U0 ("промолчать"). Доминирует - это значит, что при каждом фиксированном неизвестном значении V1 или V2 стратегия U1 лучше, чем U0, действительно: 0 < 1 и 6 < 8.
Аналогично для второго игрока стратегия V1 доминирует стратегию V0.
2) Кроме того, пара (U1, V1) находится в ситуации равновесия - это когда обоим игрокам невыгодно по одиночке отступать от своих стратегий. Иначе говоря, замена (U1, V1) на (U0, V1) ухудшает результат для первого игрока, а замена (U1, V1) на (U1, V0) ухудшает результат для второго игрока.
В этом смысле стратегии U1 и V1 - вполне рациональны.
Но такой результат противоречит здравому смыслу.
Из учебника [2]:
"... всё говорит о том, что наилучшими стратегиями игроков в этой игре являются их гарантирующие, равновесные стратегии признания, и игроки выберут именно их. А решением этой игры будет исход, когда оба игрока признаются. Однако ведь существует исход , когда оба не признаются. Этот исход значительно более выгоден игрокам и может рассматриваться как самый лучший исход для игроков в данной игре с точки зрения здравого смысла. Но никакие формальные соображения нас к нему не приводят.
Этот пример показывает, что справедливо следующее утверждение: ситуация равновесия, которая является центральным понятием в теории антагонистических игр, может не соответствовать представлению о справедливом решении игры и оптимальном поведении игроков в неантагонистических играх, т.е. ситуация равновесия в играх с непротивоположными интересами может не являться оптимальным исходом с точки зрения здравого смысла, а равновесные стратегии могут не быть наилучшими стратегиями для игроков.
Итак, в некооперативном варианте игры положение безнадежно. Все указывает на то, что игроки выберут свои вторые стратегии (стратегии признания)..."
Дурная игра. Наилучший исход очевиден, а прийти к нему невозможно.
Далее Хабибуллин обсуждает возможность договориться. Однако договор между игроками принять пару (U0, V0) лишь провоцирует обмануть и выкрутиться, и ничего не гарантирует.
Как же прийти к паре (U0, V0) рационально?
Когда я играл с Сашей, я размышлял так.
Буду уважать второго заключенного. Буду считать его столь же умным, как и я. Поэтому, если я найду оптимальное решение, то и он найдет его. А значит мы придем к одной и той же стратегии. Останутся только два варианта (U0, V0) и (U1, V1). В первом варианте нам сидеть по 1 месяцу, а во втором - по 6 месяцев. Итак, выбираю U0.
Саша тоже выбрал U0.
После написания текста по анализу парадокса о двух конвертах, у меня возникла еще и такая мысль.
А что будет, если погрузиться в гипотетический ансабль повторяющихся ситуаций? Предположим, что память о предыдущих выборах сохранилась. Тогда, если я выберу U1, то никакие будущие игроки уже не согласятся на V0. И я буду до конца своих дней получать по шесть месяцев.
С другой стороны. Если я выберу U0, то приглашу будущих игроков к союзничеству. Конечно, некоторые воспользуются этим, чтобы за счет меня вылезти сухими из воды. Но многие согласятся на союз, и в среднем, я могу рассчитывать менее, чем на 6 месяцев.
А теперь, итоги голосования!
К 13.40 18.02.2013 проголосовало 115 человек + я (для четности). 96 человека выбрали U0 и 20 человек выбрали U1.
Компьютерная случайная разбивка на пары дала такой результат:
4 "рассказчика" завалили друг друга и получили по 6 месяцев.
16 "рассказчиков" посадили 16 "молчунов" на 8 месяцев, а сами выкрутились.
80 "молчунов" нашли друг друга и отсидели по месяцу.
Все-таки эта "дилема заключенного" это классический пример тогда, когда между участниками в подобной ситуации не происходит никакого обмена информации, они принимают решение не кооперироваться, и максимальная суммарная выгода не достигается. А если включать какие-то дополнительные гипотетические последствия типо уважения других или мести, то это уже совсем другая история, и в таком случае эти выгода должна быть как-то оценена "в месяцах" и включены в таблицу с условиями.
Кстати, фильм "Игры разума", как раз о том самом математике Джоне Нэше, который исследовал подобные ситуации, там есть немного на эту тему:)
"В этом смысле стратегии U1 и V1 - вполне рациональны.
Но такой результат противоречит здравому смыслу."
Мне кажется,что здравый смысл вместе отсидеть по месяцу становится здравым только в случае, если заключенных волнует судьба друг друга. Если каждого волнует только он сам, то они выберут U1 V1. К сожалению...
Выгоднее всего иметь такого Колю, который бесконечно кладёт в конверты,
в конце концов это можно потом просто поделить побратски.
Задача о заключённых:
Если это математическая задача, то она сводится к поиску минимума ущерба, который измеряется отсидкой одного чела,
который и принимает решение, а тут всяк выгоднее отсидеть 6, вместо 8 и 0 вместо 1.
Если это задача из жизни, то здравый как раз смысл подсказывает, что ущерб тут может лечь совсем не в области дней отсидки,
а об этом в условии задачи ничего не сказано.
Больше всего понравились розы!
И еще более странная закономерность: если проводить эксперимент, разрешая обоим подозреваемым свободно общаться между собой, результат остается таким же. Оба человека, даже выработав совместную стратегию поведения, в конце концов совершают предательство. Проблема заключается в том, что люди не способны полностью доверять друг другу. все говорит о том, что надо говорить...
Однако, статистика на риске говорит о том, что выгоднее молчать... Видимо сказывается некая специфика или правила "цеха" как-то так...
*****
Интересно, что значит, открыли?
"Открыли" в контексте вполне бессмысленое слово.
Толи они предположили, что так будет.
Толи им об этом кто то рассказал.
толи они провесли исследование среди заключеных-
абсолютно непонятно.
И по ссылкам Дрешер-Флуд тоже неясно.
Как же это они "открыли"
Может, взяли много пива, посидели до упора- и -" открыли" ?
Тот, кто напился сильней, пробормотал, тот, кто был трезвей- записал а салфетке окурком :))
Приведу её начало:
Дилемма заключённого (англ. Prisoner's dilemma, реже употребляется название «дилемма бандита») — фундаментальная проблема в теории игр, согласно которой игроки не всегда будут сотрудничать друг с другом, даже если это в их интересах. Предполагается, что игрок («заключённый») максимизирует свой собственный выигрыш, не заботясь о выгоде других.
Суть проблемы была сформулирована Мерилом Фладом (Merrill Flood) и Мелвином Дрешером (Melvin Dresher) в 1950 году. Название дилемме дал математик Альберт Такер (Albert W. Tucker).
В дилемме заключённого предательство строго доминирует над сотрудничеством, поэтому единственное возможное равновесие — предательство обоих участников. Проще говоря, не важно, что сделает другой игрок, каждый выиграет больше, если предаст. Поскольку в любой ситуации предать выгоднее, чем сотрудничать, все рациональные игроки выберут предательство.
Ведя себя по отдельности рационально, вместе участники приходят к нерациональному решению: если оба предадут, они получат в сумме меньший выигрыш, чем если бы сотрудничали (единственное равновесие в этой игре не ведёт к Парето-оптимальному решению). В этом и заключается дилемма.
В повторяющейся дилемме заключённого игра происходит периодически, и каждый игрок может «наказать» другого за несотрудничество ранее. В такой игре сотрудничество может стать равновесием, а стимул предать может перевешиваться угрозой наказания (с ростом числа итераций равновесие Нэша стремится к Парето-оптимуму).
Там еще много интересного. Особенно интересно о повторяющихся играх, когда игроки постепенно переходят к сотрудничеству. :)
- добрым (первым не предавать)
- мстительным (наказывать за предательство)
- прощающим (прерывать серию взаимных предательств и начинать сотрудничать)
Теперь понятно как надо себя вести в разных ситуациях!
откуда взялась уверенность, что заключенные будут вести себя именно так?
После 2й мировой в американской психологии было сильно направление бихевиоризма, фактически , дрессировки и контроля,
предполагалось, что представители низших классов общества умственно и морально неполноценны.
Может, отсюда?