Специально для Риска! Трактат о распределении козырей у вистующих и о связанных с этим рисках.

Этот трактат, мои уважаемые читатели, я осмелюсь начать с изучения распределения трех козырей у двух вистующих.
1. Распределение трёх козырей между вистующими.
Итак, у игрока 5 козырей. Как распределяются 3 оставшихся козыря между первым вистующим А и вторым вистующим В ?
Пусть случайная величина X выражает число козырей у вистующего А. Прежде, чем приступить к расчету вероятностей, напомним читателю формулу для вычисления числа сочетаний:
C(n,m) = n! / (m! * (n-m)!),..................................................................................... (1)
где m! - произведение целых чисел от 1 до m >= 1, по определению, 0! = 1. Например, число сочетаний из 4-х букв A, B, C, D по 2 штуки равно шести. Мы все эти сочетания можем выписать: (А,B), (A,C), (A,D), (B,C), (B,D), (C,D). Других пар не существует. Формула (1) дает тот же результат:
C(4,2) = 4! / (2! * 2!) = 1 * 2 * 3 * 4 / ( 1*2*1*2 ) = 6.
Теперь применим формулу (1) для вычисления распределения случайной величины X. Итак, у игрока 10 карт, еще две карты ему известны, они в скинутом прикупе. Оставшиеся известные 20 карт распределены неизвестным образом по 10 карт между вистующими A и B. Число сочетаний, которые возможны у вистующего A, равно C(20,10) – вот столько вариантов расклада карт между двумя вистующими.
Теперь выпишем только те сочетания из числа C(20,10), в которых присутствуют 2 козыря. Таких сочетаний меньше. Две карты у вистующего А – это козыри. Выбрать 2 козыря из трёх можно тремя способами: C(3,2) = 3. Остальные 8 карт выбираются из оставшихся 17-ти некозырных карт вот таким числом способов: C(17,8). Поэтому число всевозможных двухкозырных сочетаний у вистующего А равно C(3,2) * C(17,8). Считая все сочетания равновероятными, получим формулу вероятности того, что случайная величина X равна 2.
P{X=2} = C(3,2) * C(17,8) / C(20,10) = 15/38.
В общем случае, вероятность того, что у вистующего А будет k козырей, выражается формулой:
P{X=k} = C(3,k) * C(17, 10-k) / C(20,10),................................................................ (2)
где k принимает значения от 0 до 3, включительно. Результаты расчета по формуле (2) представлены в таблице:
Таблица 1.
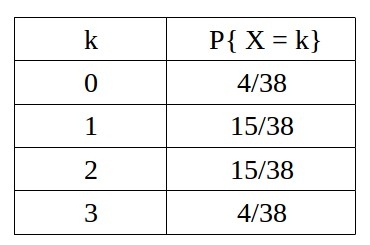
Теперь мы можем оценить размер выигрыша или проигрыша, взвешивая последствия с вероятностями 4/38, 15/38, 15/38 и 4/38. Например, мы можем вычислить цену для следующей лотереи. Она типична для тех игроков, которые не закладываются на семирной игре на три козыря у одного из вистующих.
Таблица 2.

Математическое ожидание выигрыша (средний выигрыш) в этой лотерее
M(W) = -58 * 4/38 + 18 * 30/38 + 18 * 30/38 – 58 * 4/38 = 2 виста.
Итак, цена такой лотереи +2 виста.
2. Распределение четырех козырей между вистующими.

Лужицкий, Арпад, Стариков, Студенин. Фото Николая Бархатова взято отсюда.
Перейдем к изучению распределения 4-х козырей между двумя вистующими A и B. Как и прежде, пусть X – случайная величина, выражающая число козырей у вистующего A. Действуя аналогично, как в разделе 1, получим формулу:
P{X=k} = C(4,k) * C(16, 10-k) / C(20,10),..............................................................(3)
где k принимает значения от 0 до 4, включительно. Результаты расчета по формуле (3) представлены в таблице:
в таблице:
Таблица 3.

“Нет повести печальней в этом мире, чем козыри четыре на четыре” - эти замечательные слова неизвестного поэта соответствуют случаям X = 0 или X = 4. Сконструируем лотерею, когда в этом крайне неблагоприятном раскладе игрок остается в шестерной игре без одной или даже без двух взяток.
Вот, что будет с вами, если вы играете шестерную игру в надежде, что козыри между вистующими разделятся пополам.
Таблица 4.

Математическое ожидание выигрыша в этой лотерее
M(W) = -42,5 * 14 / 323 - 12 * 80 / 323 + 7 * 135 / 323 - 12 * 80 / 323 - 42,5 * 14 / 323 = -6,7 виста.
А теперь рассмотрим такую весьма реалистичную лотерею. Она характерна для игрока, который закладывается на распределение козырей "три к одному", но не принимает в расчет редкий случай, когда все 4 козыря находятся у одного из вистующих.
Таблица 5.

Математическое ожидание выигрыша в этой лотерее
M(W) = -31 * 14 / 323 + 7 * 80 / 323 + 11,5 * 135 / 323 + 7 * 80 / 323 - 31 * 14 / 323 = 5,59 вистов.
Вывод для начинающих. Не упускайте возможности вистовать. В весьма достоверной модели шестерной игры вы приобретаете, в среднем, по 5,6 вистов за игру. Но зачастую, вы ленитесь и отказываетесь вистовать, упуская при этом, например, 4 или 6 вистов, то есть, величину соизмеримую с бонусом основного игрока.
ПРОДОЛЖЕНИЕ

Что курили?
Но к кучерявости «трактата» вариант Сергея однозначно лучше подходит.
О себе, в этом плане.
В преферанс когда-то играл, математике не чужд – как-то даже первым раскрутил одну из «загадок» Лебедева. Но было это пару лет назад.
Вот и думаю: то ли я стареть уж совсем стремительно начал, то ли интеллектуальный уровень РИСКа резко возрос?
А может, вопрос рассчитан на этих самых, «с девятью виртуальными жизнями»?
Есть правда сильные сомнения, что они слышали слово преферанс.
Как для прикола, так и половины текста бы хватило.
Наиболее вероятно, что это своеобразный фон для замечательных снимков.
Этот трактат ни в коем случае не является фоном для замечательных снимков. Это самостоятельный чисто походный продукт, достойный приложения к отчету о походе.
После завершения успешной во всех отношениях единички на майские праздники мы поселились в Гаграх. Там, в перерывах между экскурсиями и купанием, я научил студентов первокурсников и второкурсников играть в преферанс.
А уже в поезде я решил, что их надо еще поучить теории вероятностей и теории статистических решений. Тогда я начал писать этот трактат.
В следующем походе мы будем изучать основы общей топологии. Это будет 2-ка в Алае, в июле месяце.
Значит, для тех, которые «с девятью виртуальными жизнями», но отобранных и обученных.
И где ж вы их в таком количестве обнаружили?
Не так давно общался с одним «не последним» человеком в этой системе (было дело, в одной связке ходили). Так он, не взирая на мизерную зарплату (по его меркам), «подрабатывал» завкафедрой в одном из московских «системообразующих». И лишь для того, чтоб найти хоть пару голов пригодных к умственной работе.
И я ему верю.
О том, что сам работаю с «надеждой нации» уже молчу.
И территориальная принадлежность здесь принципиального значения не имеет.
Это была бы откровенная обдираловка, даже при расчете по сочинской системе. Я там по 200-400 вистов выигрывал на 20-ке.
Очень смутное это понятие.
В моё время считалось - на деньги.
(Хотя изначально, по наивности, думал тоже, что «просто так».)
А сейчас, если полазать по «интырнету»...
Очень крутые варианты встречаются.
А игра "на интерес" возможна. Преферанс тем и хорош, что можно суммировать результаты за большое количество игр, а расплачиваться после похода, хотя бы и напитками.
Замечательная фраза была в старинном трактате о расчете."Наконец полученный результат следует умножить на оговоренную цену, чтобы узнать, сколько следует уплатить за полученное удовольствие"
В продолжении трактата будет изучаться совместное распределение козырей и второй сильной масти. Вот там будет гораздо интереснее! Понятно, что если сильная масть и козыри у вистующих на одной руке - тогда труба. А если на разных руках, то можно выкрутиться даже при козырях 4 на 4.
Всегда ленился численно оценить вероятность раскладов.
На интерес - на клюкву по осени на болоте или классическое на пиво после похода в разных вариантах
Посмотрите на спортивный бридж. Там уже все сосчитали, там и правила стабильнее и все честно, как в шахматах т.к. карты не смешивают, и на них же играют на другом столе.