Математика очных чемпионатов

После прошедшего недавно чемпионата Москвы хочется рассмотреть вопрос, на который мало кто обращает внимание, хотя он, на мой взгляд, является базовым, определяющим куда и как будут ходить спортсмены на чемпионате. Я буду писать про Малые Горы, так как хорошо представляю себе откуда взялись его формула и рейтинг, присутствовал при всех изменениях и знаю, чем руководствовались при этом организаторы. Все написанное, конечно, относится к любым очным соревнованиям.
На чемпионатах считают баллы. Баллы получаются из рейтинга маршрутов и времени прохождения посредством формулы. Из этого следует, что рейтинг и формула – это важнейшие параметры, которые определяют тактику спортсменов. И было бы очень здорово пользоваться именно этими параметрами, а не призывами к фэйр плей и аккуратному хождению.
С рейтингом обычно все плохо. Толковый рейтинг выстроится, если проводить чемпионат в одном и том же месте много лет подряд. Да и то он будет именно что толковый, а не безупречный – рейтинг зависит от формулы, а маршруты имеют тенденцию упрощаться. Единственное, что хотелось бы предложить – сразу после чемпионата, по горячим следам, собирать всех участников и вносить изменения в рейтинг, когда никакого корыстного интереса нет, а воспоминания свежи. На благо потомкам.
С формулой все гораздо интереснее.
Я сразу оговорюсь, что речь тут пойдет про спринт, для марафона формула в виде суммы баллов лично у меня вопросов не вызывает.
Очень часто приходится встречаться с формулой, где что-то делят на время, то есть пользуются гиперболической функцией. Выглядит она так:
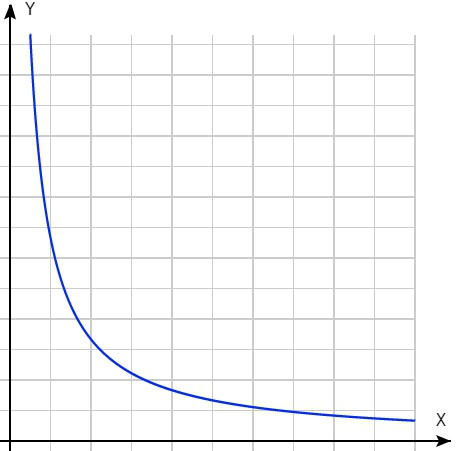
график 1
Те, кто организуют соревнования, видят, наверное, вот этот кусочек:
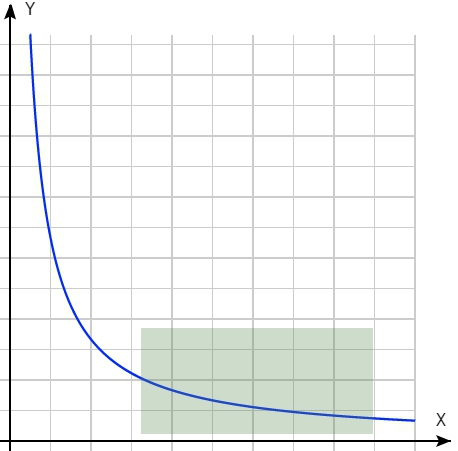
график 2
Спортсмен видит это:
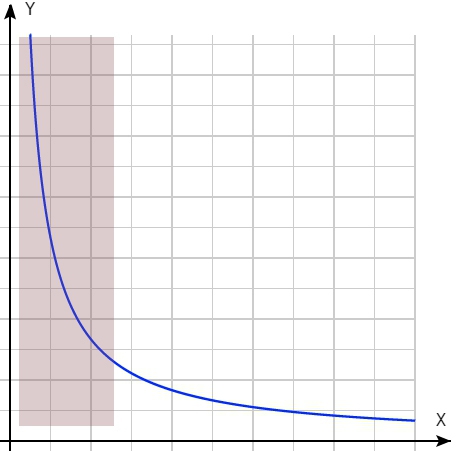
график 3
И тут же прикидывает, получится у него в красную зону попасть или нет. Если найдет, то разживется баллами от души. И это будет результатом не его восходительских навыков, а аналитических способностей (причем скорее всего стороннего советчика).
Если хочется примеров, то вот: на прошедшем недавно чемпионате Москвы использовалась формула Б=R+0.03*R*Lсложн*(1/t) (время в формате часы).
Возьмем для примера маршрут Центр. Lсложн 300 метров, рейтинг 4.5. Сергей Нефедов и Слава Титов добились времени час ноль пять, посчитаем их небожителями и допустим для обычных людей результат 1.5 часа (речь про скоростной забег после насоса). Формула покажет 31.5 балл. У победителей с их сумасшедшими (для онсайта) временами на гиперборее и СД на балл меньше сумма двух маршрутов.
Лично меня бы устроила и линейная функция:
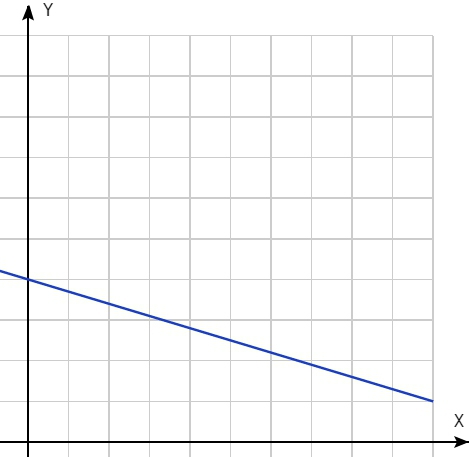
график 4
Но если это скучно, то можно использовать и функции повеселее:
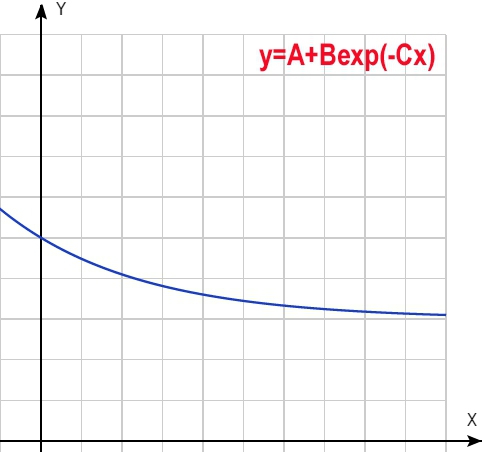
график 5
Можно, кстати, и гиперболой воспользоваться, просто сдвинуть неудобную часть в область отрицательных значений аргумента:
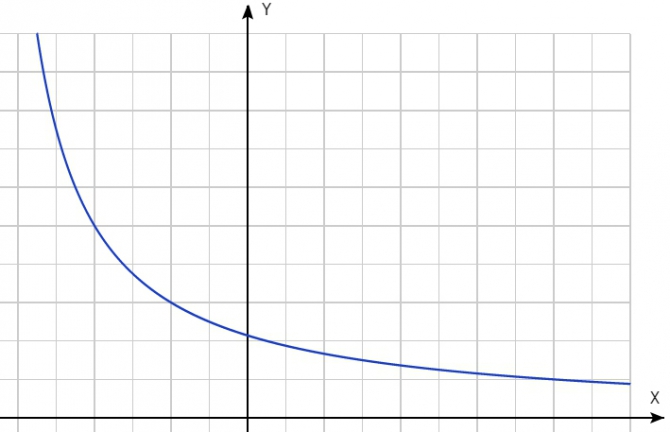
график 6
Больше всего мне нравится такой вариант:
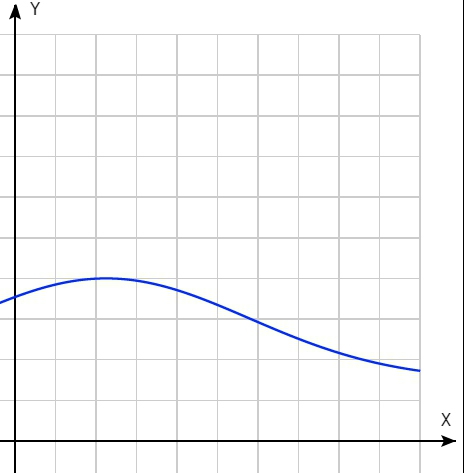
график 7
Который сразу говорит, что будешь торопиться – недоберешь баллов.
Ну или что хочешь баллов – лезь сложное, а не беги простое.
Тут сразу можно услышать возражения – а что, если спортсмены попадут вдруг до горба, им что, сидеть куковать на полке под вершиной? Если такой аргумент кажется стоящим, то можно рассмотреть такой вариант:
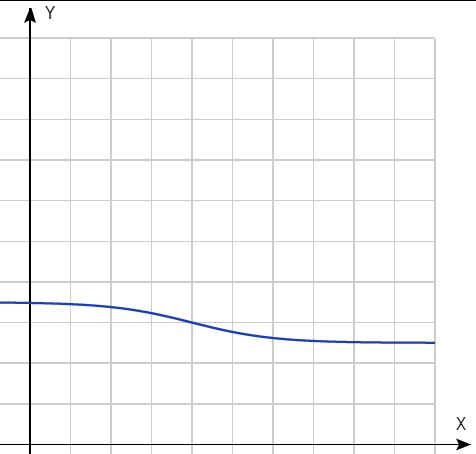
график 8
Краткий пример с прошедшего Чемпионата Москвы 2015:
Представьте, что вы выбираете себе маршрут для восхождения. Вы смотрите на формулу и рейтинг:
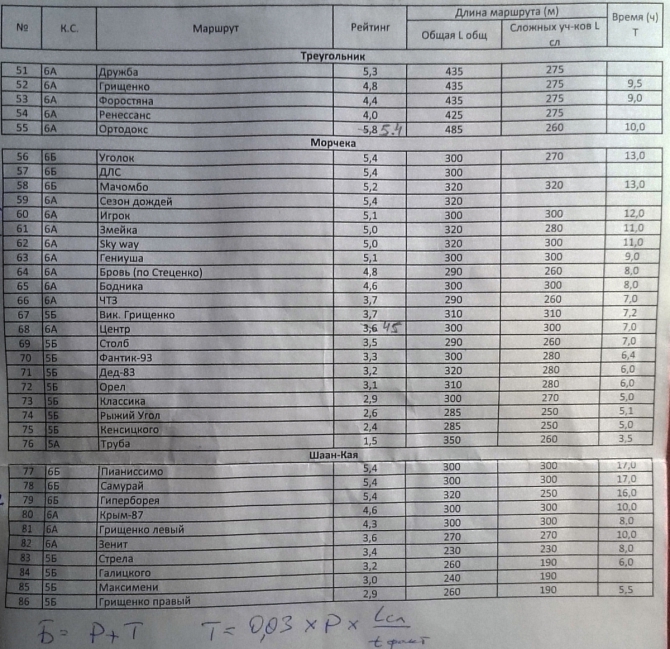
Понятно куда лезть? Графики выглядят вот так:
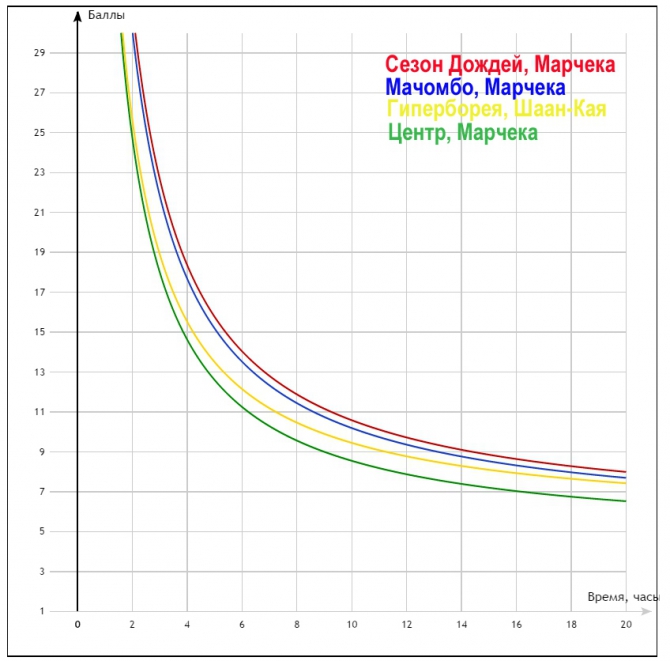
график 9
Обратите внимание на Мачомбо с рейтингом 5.2 и Гиперборею с рейтингом 5.4
Если кто-то хочет нарисовать свой график и предложить что-то, то я пользовался вот этим сервисом , потом принт скрин и фотошоп.
Большое спасибо спонсорам чемпионата:


А если у нас недостаточно сложных маршрутов, значит кто то жестко накосячил с выбором района, и соревнования рискуют стать очень отстойными, посему лучше в них и вовсе не участвовать.
Идея: выбрать формулу при которой такого не произойдет. Свои варианты Игорь написал. На мой взгляд экспонента выглядит разумно.
"Да это же и ежу понятно. Девочки, вам все понятно?" ))
И вот тут хочется Васе сказать: построй графики зависимости баллов от времени и все сразу увидишь. На одном графике нарисуй несколько маршрутов разным цветом, ноутбук с экселем сейчас в горах есть у каждого второго.
И организаторам, которые всё проработали с калькулятором в руках (в лучшем случае) хочется сказать то же самое.
А если Вася построит график (ну или ему хватит терпения 2 часа кнопки нажимать на калькуляторе), то он увидит, что скоростной забег по пятерке стоит подороже, чем качественное (и в хорошем темпе) восхождение по высокой и трудной шестерке. После чего выложит из рюкзака еду, воду, бивуак, половину железа, перекрестится и помчится устанавливать рекорд. А судьи будут сидеть под маршрутом с биноклем и молиться, чтобы раб Божий Василий не расстался с жизнью или остатками здоровья.
И чтобы тупые мысли Васину голову не посещали, хорошо бы формулу изменить.
Причем сделать это так: нарисовать график руками и попросить знающих людей смоделировать его какой-нибудь функцией.
Вот как-то так, если простыми словами.
Жаль Игорь не пронумеровал свои графики.
Но упрощая можно сказать, что я вижу на них гиперболу и линейную функцию.
Остальные графики хорошо интерполируются линейной функцией.
На одном, правда, есть небольшой горбик сомнительного свойства (забьем на него).
Поэтому рассмотрим подробнее два графика: гиперболу и прямую.
В общем виде они задаются следующими формулами:
1. B = R + k*R/T гипербола
2. B = R - T прямая
В - баллы, R - рейтинг маршрута, Т - время прохождения (например в часах), k - коэфф.
В чем же сакральный физический смысл этих двух формул:
1. В = R + k*R/T
Пройдя маршрут, команда получает рейтинг R + бонус за скорость. Нетрудно понять, что R/T это есть скорость команды - сколько единиц рейтинга команда пролезает в час. Если все маршруты у нас примерно одинаковой сложности в качестве R можно использовать просто длину маршрута, тогда R/T это и есть в чистом виде скорость (метров в час).
k это коэффициент, который определяет величину бонуса за скорость. Вклад скорости можно увеличивать и уменьшать. В марафоне k=0 - бонус за скорость отсутствует.
Сейчас в техническом классе мы обкатываем как раз эту формулу. Ее особенность в том, что каждый маршрут конкурирует со всеми остальными. На самом дешевом маршруте можно победить самый дорогой, если скорость стремится к бесконечности (время стремится к 0). Весь вопрос, как обычно, упирается в балансировку рейтингов ))
Можно сказать, что эта формула подходит для хорошо освоенных районов с безопасными маршрутами, в которых нет достаточного количества сложных маршрутов с высокими рейтингами. Кому не достался дорогой маршрут, может побороться на дешевом. Или намеренно выбрать дешевый, делая ставку на фаст-н-лайт.
С другой стороны, если мы зададим поменьше коэфф k, уменьшая вклад скорости, мы получим формулу близкую к той, которую предлагает Саша Кленов - часы и минуты не будут иметь значения т.к будут отбрасываться при округлении )) Правда, тогда конкурировать на дешевых маршрутах станет нереально.
2. В = R - T
Это самая простая и прекрасная формула. Время здесь выступает в качестве штрафа. Пройдя маршрут, команда получает рейтинг R минус штраф за время. Если будет долго ковыряться уйдет в минуса. Но что там происходит с аутсайдерами, никого особо не интересует. Все следят за лидерами ))
Умножим нашу формулу на -1:
B = T - R
В этом случае победителем нужно считать того, кто наберет наименьшее число баллов. Это очень напоминает нам формулу по которой соревнуются на школе, не так ли? Если команды проходят одни и те же маршруты, рейтинги у всех одинаковые, они просто отбрасываются. Побеждает тот, у кого меньше сумма времен.
В общем случае результат команды есть сумма времен уменьшенная на сумму рейтингов пройденных маршрутов. Просто и эффективно. Основным показателем здесь является время, а рейтинг выступает дополнительным бонусом, который уменьшает итоговую сумму.
Однако, вернемся к начальной формуле B = R - T. Понятно, что они равнозначны, но почему-то проще рассуждать в понятиях "у кого больше баллов, тот и победил".
Баллы, получаемые за маршрут, здесь ограничены рейтингом. Даже если команда залетит на вертолете, больше чем R она не получит (как в марафоне). Поэтому дешевые маршруты не могут конкурировать с дорогими, если в зачет идет ограниченное количество маршрутов (формула спринта).
Формула B = R - T подходит для районов с большим количеством однотипных маршрутов. Точность расстановки рейтингов не так важна. Главное, чтобы было достаточное количество дорогих маршрутов с близкими (одинаковыми) рейтингами. Это бега на время.
Или другой вариант - командам предоставляется несколько маршрутов. Каждая команда, проходит каждый маршрут, времена складываются, рейтинги, понятно дело, отбрасываются. Это вариант школы. Тут нужно иметь достаточный запас по времени проведения соревнований и обеспечить новизну, чтобы все лезли онсайт. Хорошо подходит для новых, мало освоенных районов. Можно замутить схему с выбыванием, которую я уже когда-то описывал. Один раз мы ее даже опробовали на ЧР в Ахмет-Кае. Другой пример проведения - Афтепати осеннего ЧР-2014 в Крыму. Вроде бы народу понравилось. Хорошо работает, когда мало команд (москвичам на заметку).
Как умел разжевал. Заодно и сам стал лучше понимать. Спасибо Игорю за поднятую тему.
Мне кажется для такого района, как Каравшин (где сложность маршрутов очень разная) неправильным то, что «каждый маршрут конкурирует со всеми остальными». Лидеры должны лазить на сложные маршруты.
Короче, если сдвинуть гиперболу (например, считать время не от 0, а от 1) или подобрать похожую экспоненту – получится то, что надо. В этом случае будет известен максимум баллов для каждого маршрута. Таким образом, можно делать простые маршруты заведомо невыгодными и в то же время оставить место для поощрения рекордных скоростей, регулируя крутизну графика.
Как только обнаруживается переоцененный маршрут на котором можно по легкому срубить баллов, все команды начинают ломиться на него. И не важно какая у тебя формула - прямая, гипербола, экспонента или просто сумма рейтингов.
Что касаемо Каравшина. Там был переоценен, например, маршрут Тимофеева на Асан. Многие команды его прошли. Но получить на нем супербаллы смогла только одна команда - победители.
Это как сказать. Если налажать с рейтингом при линейной функции - получишь просто переоцененный маршрут, если залажать при гиперболе можно получить лютую хрень (пример Игоря с Центром как раз из этой оперы).
Так что, если не умеешь оценивать рейтинги, лучше не берись.
Или бери формулу попроще (без рейтингов).
В Каравшине были косяки с рейтингами, но не критичные (имхо).
Вполне рабочие, человеческие косяки ))
Мне больше нравится графики 5 или 6, если считать сверху. График с горбом или даже с горизонтальным началом неспортивен. Хорошее время на маршруте должно вознаграждаться, но не должно быть настолько решающим (график не должен быть слишком крутым). Думаю, в начале (от 0 часов до среднего времени хорошей группы на маршруте) он должен идти под углом примерно 45 градусов, затем постепенно выполаживаться до горизонтали.
почему бы не давать временной бонус не за весь маршрут, а за определенный участок(участки). То есть, чтобы избежать скоростного бега без страховки по огородам, даем бонус за время прохождения ключевого участка(участков) и его прибавляем к рейтингу маршрута(который оценивает общую трудоемкость). Это позволит спортсменам сконцентрироваться на сложных спортивных участках и увеличить безопасность за счет отсутствия постоянной и продолжительной спешки. Более того, это может дать возможность не ломиться в плохую погоду при многодневных маршрутах в больших горах.
Еще, для зрителей весь день смотреть тяжело не отрываясь(транслировать, так вообще никак), а так, сильная команда на втором бонусном участке - все камеры и бинокли смотрят. Короткие участки можно транслировать и судить строже огрехи в страховке. Например, отсмотреть видео с Гопры с ключевых участков для первых 5 команд ни так и сложно. Вообще, возможность показать соревнования не только зрителям на месте важнейший момент для популяризации вида спорта. Ато сколько было в Каравшине зрителей?
Что касается формулы бонуса, то гипербола выглядит хорошо в том плане, что чем ближе к пределу, тем сложнее улучшить, и поощрять это нужно балами больше. Здесь главным становится вопрос, на какую собственно часть гиперболы лягут реальные результаты. А это не так сложно подогнать если это Крым(особенно для отдельных участков). Например, если посмотреть на кривые маршрутов с прошедших Малых гор, которые приводит Игорь, то их форма от 4 до 12 часов выглядит довольно хорошо.
В общем, энтузиасты квадрокоптеров, отзовитесь!
правда в рамках ЧРов, организуемых ФАР, подобное явное провести не возможно, так как предполагает активную судейскую работу.
to XBOST: это как раз то, о чем я и говорил, ты рисуешь формулу и по ее виду рассуждаешь, что же она значит. А я предлагаю нарисовать график, какой хочется, и под его вид подобрать формулу.
to Misha: горб и пологий старт на графиках 7 и 8 предполагается расположить в районе ненормально маленького времени, в качестве защиты от стиля восхождения, предполагающего явное пренебрежение страховкой и подразумевающего жестокий насос. Не думаю, что это актуально на текущий момент. Графики приведены скорее в качестве иллюстрации того, как можно влиять на тактику спортсменов формулой.
По поводу графиков 5 и 6:
первый задается функцией B=R+k1*exp(-k2*t)
Все хорошо, только экспоненту на непродвинутом телефоне не посчитаешь.
формула второго отличается от текущей формулы чемпионата еще одним коэффициентом:
В = R + k1*R/(k2+T)
Эти графики в выбранной области от прямой отличаются не сильно.
Не думаю, что есть смыл заморачиваться с экспонентой. Мне, по крайне мере, не очевидно, чем она лучше прямой в данном примере.
На рисунке ниже: красная гипербола (формула 1 у Олега) и она же немного сдвинутая (синий график). Всё тот же резкий рост баллов при малом времени. Но мы добавляем ко времени команды пару часов, что для длинного маршрута практически не изменяет итоговые баллы, а для простого заметно их уменьшает. Таким образом, сдвигаем приоритеты в сторону более сложных маршрутов. Сильная команда сможет обогнать более слабую даже на простом маршруте, но за призы будут бороться только сложные маршруты. "Сложный" и "простой" - я имею ввиду разницу рейтингов в разы.
Ну и регулярное изменение пресловутой "формулы подсчёта" не даёт времени собрать "статистику". Гораздо полезнее зафиксировать формулу на олимпийский цикл и посмотреть, к чему это приведёт.
А то народ мечется, как футболисты. То играли весна-осень, было плохо. Сейчас играют осень-весна - опять не здорово. Может быть и тут не то в условиях меняют?
Чем больше заинтересованных людей выразит свое мнение в спокойной обстановке,
тем больше шанс, что это мнение учтут.
По поводу набора статистики - вроде у всех один и тот же вопрос встал, нашли больную точку.
Будем еще пару лет ждать?
А гарантии, что вы нашли больную точку - нет.
где можно к чему-то прийти.
Можно выразить свое мнение и надеяться, что его заметят и учтут при принятии решения.
0) дополнение - предлагается для каждого маршрута ввести Tбезопасное - условное время, за которое этот маршрут может безопасно (и особо не спеша, но и не копаясь) пройти подготовленная связка.
Рассчитывать Tбезопасное можно, например, как сумму произведений длин различных участков маршрута на коэффициенты, пропорциональные сложности.
Т.е. если на условном маршруте 100 метров III скал и 100 метров IV+, а коэффициенты Kiii = 1/(10 метров в минуту на связку), Kvi+ = 1/(2 метра в минуту на связку), то
Tбезопасное = 100 * 0.1 + 100 * 0.5 = 60 минут.
Основания для определения B(t) (функции результат от времени):
1) производная B(t) при T<<Tбезопасное должна быть нулевой (или очень маленькой) - пролезете вы наш условный маршрут за 30 минут или за 40 - разницы в баллах никакой.
2) производная B(t) при T~Tбезопасное должна быть большой - чтобы близкие по силе (и по времени на маршруте) связки легко "раскладывались" в итоговом протоколе - т.е. имели достаточно большие разницы в баллах
Я бы взял какую-нибудь ступенчатую функцию из математики - логистическую функцию, к примеру:
B = 2R - R/(1 + exp(-10(t-Tбезопасное)))
Для маршрута с рейтингом 1 и Тбезопасное = 1 час:
максимальный возможный балл = 2
минимальный возможный балл = 1
при прохождении за 1 час связка получает 1.5 балла, при прохождении за полчаса - 1.99 балла, за 45 минут - 1.92 балла.
предполагаемое время/Тбезоп коэффициент
<=0.4 2.0
0.5 1.99
0.6 1.98
0.7 1.95
и.т.д
Я такую кривую нарисовал гиперболическим тангенсом (график 8).
В графике просматривается такая идея: за баллы можно бороться в некотором диапазоне времени, выпадение из этого диапазона (выбор слишком простого или слишком сложного маршрута) невыгоден.
Предполагаемое время прохождения обычно считают на всех чемпионатах, в посте есть сфотографированный лист с рейтингами маршрутов, в последней графе - как раз оно.