Анализы парадокса о двух конвертах и задачи о двух заключенных.

ПАРАДОКС О ДВУХ КОНВЕРТАХ.

Коля положил в два одинаковых почтовых конверта некоторую сумму денег, причем в один из них ровно в два раза больше, чем в другой. Потом он подбросил монетку и, повинуясь случаю, один из конвертов вручил Васе, а другой Пете.

Вася открыл конверт, пересчитал деньги и подумал так: "У меня в конверте сумма X. Значит, с вероятностью 0.5 в конверте у Пети лежит сумма X/2 и с вероятностью 0.5 он обладает суммой 2X. Выгодно ли мне меняться? Ожидаемый выигрыш от обмена конвертами равен: 0.5 * (X/2 - X) + 0.5 * (2X - X) = 0.25 * X > 0. Значит, меняться выгодно!"

Аналогично может рассуждать и Петя. Получается, что меняться выгодно обоим. Но ведь, это же лажа!

Анализ парадокса о двух конвертах.

Как рассуждает Вася?
Он рассчитывает ожидаемый выигрыш от обмена конвертами. Такое среднее в теории вероятностей называется математическим ожиданием выигрыша.

Какая интерпретация полученной величины?
Интерпретация достигается мысленным погружением в гипотетический ансамбль повторяющихся ситуаций.

Например, если вы обладаете лотерейным билетом, который выигрывает 100 рублей с вероятностью 0.5, математическое ожидание выигрыша равно 0 руб. * 0.5 + 100 руб. * 0.5 = 50 руб. При многочисленных играх с билетом такого номинала вы получите примерно N* 50 руб., где N - число игр, причем, чем больше игр, тем меньше относительная ошибка в прогнозе дохода. Если N - миллион, то ваш доход будет отличаться от 50-ти миллионов рублей менее, чем на 0.3 процента (0.003) с вероятностью 0.997.

Вот и Вася мысленно погружается в гипотетический ансамбль повторяющихся ситуаций с обменом конвертами.
Но каков источник случайности в этих будущих его играх? Судя по тому, как он ведет расчет, единственным источником случайности он считает монетку, которую подбрасывает Коля. А количество денег в конверте X, он не усредняет по какому-либо распределению вероятностей и считает его, как бы, фиксированным.

Однако величина X Васе заранее неизвестна, как и все её будущие значения. Такое частичное осреднение, которое произвел Вася, при фиксированном X, в теории вероятностей называется условным математическим ожиданием, "математическое ожидание при условии, что величина X принимает наблюдаемое значение".

Является ли условный ожидаемый доход критерием рационального выбора?

Да, если мы имеем дело со статистически определенной ситуацией, т.е., когда вероятности всех фигурирующих в модели событий заранее известны.

При наличии известного распределения для X математическое ожидание выигрыша равно условному ожиданию, усредненному по распределению случайной величины X. Поэтому, если условное ожидание выигрыша при каждом фиксированном X максимально, то максимальным будет и безусловное ожидаемое значение выигрыша.

Может быть на это рассчитывал Вася?
Но тогда он неправильно посчитал свой выигрыш. Он не учел распределения величины X.

А без этого нельзя. Предположим, что используемый Колей капитал не превосходит 300 рублей. К примеру, пусть сумма денег в обоих конвертах Z распределена равномерно от 0 до 300 рублей. Тогда, если Вася увидел в своём конверте 110 рублей, он уже не должен меняться. Ведь у Пети может быть только 55, но никак не 220 рублей (110 + 220 > 300).

А между тем Васин расчет показывает положительный условный выигрыш при любом значении X, и при любом распределении X.

Чему же соответствует Васин расчет? Какому гипотетическому ансамблю?

А вот какому. Васе постоянно кладут в конверт 100 рублей, а Коля с вероятностью 0.5 кладет в конверт Пети то 50, то 200 рублей. Но это несимметричная ситуация, и никакого парадокса нет. Васе каждый раз выгодно меняться, а Пете нет.

100 рублей - это к примеру. Речь может идти о 200 рублей или иной сумме, но, главное, что эта сумма в гипотетическом ансамбле повторяющихся ситуаций остаётся фиксированной.

Однако это не интересный случай.

Исследуем задачу при некоторых стандартных распределениях суммы денег Z в двух конвертах.
Оказывается, что парадокс в некотором смысле сохраняется, и обоим игрокам при определенных ограничениях выгодно меняться. В Википедии ничего не говорится о возможности такой ситуации.

Итак, пусть сумма денег Z, которую Коля тратит на эксперимент, случайна и имеет функцию распределения F(z). Пусть независимая от Z бинарная случайная величина T принимает значения 0 или 1 с вероятностями 0.5 и отражает, кому досталась меньшая часть денег, т.е. Z/3: если Васе, то T = 0, если Пете, то T=1.

Пусть X - сумма в конверте Васи. Найдем функцию G(x) распределения случайной величины X.

G(x) = P{ X < x } = P{ X < x, T = 0} + P{ X < x, T = 1} = P{ Z/3 < x, T = 0} + P{ 2Z/3 < x, T = 1} = P{ Z < 3x, T = 0} + P{ Z < 3x/2, T = 1} = 0.5 * F(3x) + 0.5 * F(3x/2).

Дифференциируя функцию распределения, найдем плотность распределения случайной величины X.

g(x) = 1.5 * f(3x) + 0.75 * f(3x/2),

где f(z) - плотность распределения случайной величины Z.

По формуле Байеса найдем условные вероятность (при условии X), что к Васе пришла меньшая сумма денег Z/3 или большая сумма денег 2Z/3.

P{ T = 0 | X } = f(3X) / [f(3X) + 0.5*f(3X/2)]

P{ T = 1 | X } = 0.5* f(3X/2) / [f(3X) + 0.5*f(3X/2)]

Как видно, эти вероятности вовсе не равны 0.5.

Условное математическое ожидание выигрыша Васи при обмене равно

Q(X) = X * P{ T = 0 | X } - 0.5 * X * P{ T = 1 | X } = X * [f(3X) - 0.25*f(3X/2)] / [f(3X) + 0.5*f(3X/2)].

Условный ожидаемый выигрыш положительный, если и только если 4 * f(3X) > f(3X/2).

Оптимальная стратегия Васи:

!!!! Меняться, если 4 * f(3Х) > f(3X/2),
!!!! Не меняться, если 4 * f(3Х) < f(3X/2).

Рассмотрим два примера:

1) Пусть Z - равномерно распределена в интервале от 0 до H = 300 руб.

Для такого распределения нетрудно посчитать, что
оптимальная стратегия Васи:

!!!! Меняться, если X < H/3 = 100 руб.,
!!!! Не меняться, если X > H/3 = 100 руб.

Ожидаемый выигрыш при этом равен H/16 = 18.75 руб.

2) Пусть Z - распределена экспоненциально с математическим ожиданием S = 150 руб.

И для этого распределения нетрудно посчитать, что
оптимальная стратегия Васи:

!!!! Меняться, если X < 2S * ln(4) / 3 = 138.6 руб.,
!!!! Не меняться, если X > 2S * ln(4) / 3 = 138.6 руб.

Ожидаемый выигрыш при этом равен S(1 + 2ln(4) / 3) / 32 = 9.02 руб.

Но ведь и у Пети тоже самое! Парадокс сохранился?

Вовсе нет. :)

Оптимальная стратегия Васи действительно оптимальна, если Петя ему не противодействует и соглашается на все обмены, которые ему предлагает Вася.

При такой пассивной со стороны Пети игре Вася действительно выигрывает с каждым обменом в среднем по 18.75 руб. при равномерном распределении и по 9.02 руб. при экспоненциальном.

И эти числа подтвердились на компьютере методом Монте-Карло!

И Петя посчитает для себя такой же положительный ожидаемый выигрыш. И этот расчет тоже будет справедлив только при пассивной игре Васи.

А что же получится при активной игре обоих игроков?

Часть выгодных для Васи обменов забракует Петя, потому что по его оптимальному критерию некоторые предложенные Васей обмены будут невыгодными. С другой стороны, часть выгодных для Пети обменов забракует Вася. В итоге, выигрыш каждого будет равен нулю. И это тоже подтверждено на компьютере методом Монте Карло.

Вот такое получилось интересное исследование.

Там обнаружилась еще одна интересная игровая деталь.
Но об этом, если и расскажу, то в другой раз.

Программа статистических испытаний:


ЗАДАЧА О ДВУХ ЗАКЛЮЧЕННЫХ.

Два заключенных сидят в СИЗО, общаться между собой они не могут. Каждый из них знает про такой расклад:

Если оба заключенных будут молчать - обоим сидеть по 1-му месяцу.
Если оба заключенных все расскажут - обоим сидеть по 6 месяцев.
Если один из заключенных будет молчать, а другой всё расскажет - то молчуну впаяют 8 месяцев, а рассказчика немедленно отпустят.

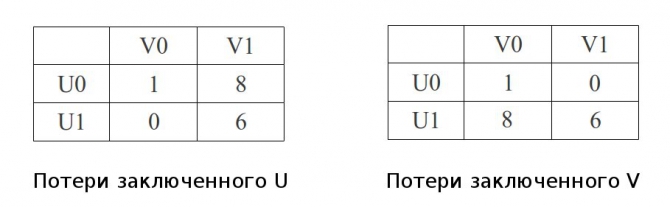
Вот как это выглядит на картинке:

В табличках прописаны сроки лишения свободы для каждого из заключенных, при вот таких действиях:

U0 - заключенный U молчит,
U1 - заключенный U говорит,
V0 - заключенный V молчит,
V1 - заключенный V говорит.

Какие решения являются рациональными в такой ситуации?

Анализ задачи о двух заключенных.

Эта задача классифицируется, как игра с непротивоположными интересами. К сожалению, я не много смогу о ней рассказать. В эту область науки я не углублялся.

Литература:

1. Ю.Б. Гермейер. Игры с непротивоположными интересами. Москва, Наука, 1976.
2. Игры с непротивоположными интересами: учеб. пособие. Сост. Р.Ф. Хабибуллин – Казань: Казан. гос. ун-т, 2009.

Первая книжка - серьезная монография.
Вторая - простенькое пособие для студентов с обзором основных постановок.

Ну что я могу сказать? Дурная задача, и в этих книжках ничего толком о ней не сказано.

1) Обращаю внимание на то, что стратегия U1 ("рассказать") доминирует стратегию U0 ("промолчать"). Доминирует - это значит, что при каждом фиксированном неизвестном значении V1 или V2 стратегия U1 лучше, чем U0, действительно: 0 < 1 и 6 < 8.

Аналогично для второго игрока стратегия V1 доминирует стратегию V0.

2) Кроме того, пара (U1, V1) находится в ситуации равновесия - это когда обоим игрокам невыгодно по одиночке отступать от своих стратегий. Иначе говоря, замена (U1, V1) на (U0, V1) ухудшает результат для первого игрока, а замена (U1, V1) на (U1, V0) ухудшает результат для второго игрока.

В этом смысле стратегии U1 и V1 - вполне рациональны.
Но такой результат противоречит здравому смыслу.

Из учебника [2]:

"... всё говорит о том, что наилучшими стратегиями игроков в этой игре являются их гарантирующие, равновесные стратегии признания, и игроки выберут именно их. А решением этой игры будет исход, когда оба игрока признаются. Однако ведь существует исход , когда оба не признаются. Этот исход значительно более выгоден игрокам и может рассматриваться как самый лучший исход для игроков в данной игре с точки зрения здравого смысла. Но никакие формальные соображения нас к нему не приводят.

Этот пример показывает, что справедливо следующее утверждение: ситуация равновесия, которая является центральным понятием в теории антагонистических игр, может не соответствовать представлению о справедливом решении игры и оптимальном поведении игроков в неантагонистических играх, т.е. ситуация равновесия в играх с непротивоположными интересами может не являться оптимальным исходом с точки зрения здравого смысла, а равновесные стратегии могут не быть наилучшими стратегиями для игроков.

Итак, в некооперативном варианте игры положение безнадежно. Все указывает на то, что игроки выберут свои вторые стратегии (стратегии признания)..."

Дурная игра. Наилучший исход очевиден, а прийти к нему невозможно.

Далее Хабибуллин обсуждает возможность договориться. Однако договор между игроками принять пару (U0, V0) лишь провоцирует обмануть и выкрутиться, и ничего не гарантирует.

Как же прийти к паре (U0, V0) рационально?

Когда я играл с Сашей, я размышлял так.

Буду уважать второго заключенного. Буду считать его столь же умным, как и я. Поэтому, если я найду оптимальное решение, то и он найдет его. А значит мы придем к одной и той же стратегии. Останутся только два варианта (U0, V0) и (U1, V1). В первом варианте нам сидеть по 1 месяцу, а во втором - по 6 месяцев. Итак, выбираю U0.

Саша тоже выбрал U0.

После написания текста по анализу парадокса о двух конвертах, у меня возникла еще и такая мысль.

А что будет, если погрузиться в гипотетический ансабль повторяющихся ситуаций? Предположим, что память о предыдущих выборах сохранилась. Тогда, если я выберу U1, то никакие будущие игроки уже не согласятся на V0. И я буду до конца своих дней получать по шесть месяцев.

С другой стороны. Если я выберу U0, то приглашу будущих игроков к союзничеству. Конечно, некоторые воспользуются этим, чтобы за счет меня вылезти сухими из воды. Но многие согласятся на союз, и в среднем, я могу рассчитывать менее, чем на 6 месяцев.

А теперь, итоги голосования!

К 13.40 18.02.2013 проголосовало 115 человек + я (для четности). 96 человек выбрали U0 и 20 человек выбрали U1.

Компьютерная случайная разбивка на пары дала такой результат:

4 "рассказчика" завалили друг друга и получили 6 месяцев.
16 "рассказчиков" посадили 16 "молчунов" на 8 месяцев, а сами выкрутились.
80 "молчунов" нашли друг друга и отсидели по месяцу.